数学徒然草:立体の体積と定積分

解答Ⅰ
複雑な人体の内部の様子を調べたい場合、CTスキャン(コンピュータ断層撮影)を使えばよく分かります。この手の問題を解く場合も、定石として、題意の立体(領域)の断面を考えます。 断面を考える場合、x , y , z のうち仲間ハズレ(よく言えば、特別な存在)の座標(=一定)での断面を考えると上手くいきます。本問の場合、z が仲間ハズレ(よく言えば、特別な存在)です。z を含む項を移項しましょう。今後、z はπのように(文字ではありますが)定数だと考えます。

この時点で、実数の2乗である左辺≧0なので、右辺も右辺≧0とならざるを得ません。よって 断面が存在するのは、-1≦z≦1 の範囲だけと分かります。
Xの2次不等式 X2≦πを解くと、-√π≦X≦√πになるのと同様に上記の2次不等式を解くと:
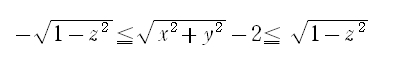
ちょっと変形します。

各辺を平方します(もともと各辺が正の数なので、平方しても不等号の向きは替わりません)。
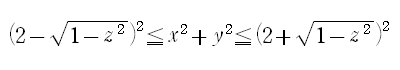
よって、
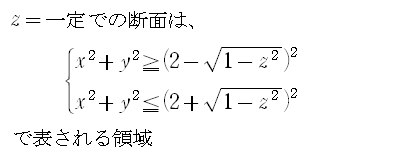
すなわち

図示すると下のようになります(境界線も含む)。

この領域の断面積を S(z) とすると

求める体積 V は、z軸に垂直な断面積 S(z) を断面が存在する z の範囲 (-1≦z≦1) で積分したものなので、

解答Ⅱ
地球を表す地図にメルカトル図法、モルワイデ図法などいろいろあるように空間の位置を表す座標系にも直交座標系、円柱座標系などがあります。直交座標系とは x軸・y軸・z軸 3本の直交する座標軸で座標を指定する座標系です。円柱座標系とは xy方向については極座標で、z座標に関しては直交座標と同じz座標を使う座標系です。
両者の間は次式によって変換されます。

この変換則によって、問題の不等式を書き換えてみましょう。

ここで、「θが現れていない」と云うことは、「θの値は任意」と云うことです。θはz軸周りの回転角なので、問題の領域は下図をz軸の周りに回転した立体になります。(つまり、題意の立体は z軸からの距離 r と z座標 z にのみに依存する立体になります。)
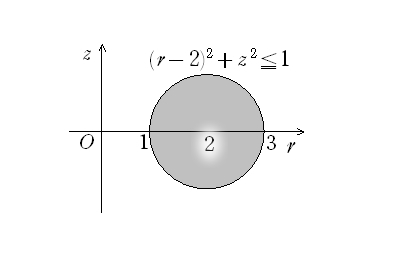
この円盤を r 軸の周りに回転した立体は、当然半径 1 の球体になりますが、今の場合、z軸の周りに回転した立体の体積を求めなければなりません。そこで次の定理を使います。
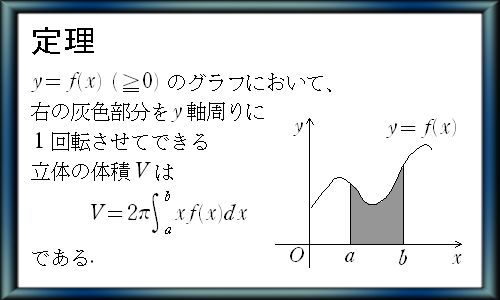
この定理を答案に使うにためには、別途、証明も書いておく必要があります。本問に適用すると次のようになります。

ここで最後の計算が本質的に 4π×πになっていますが、いわゆる「パップス-ギュルダン(Pappus-Guldinus)の定理」
回転体の体積=重心の移動距離×回転させる面の面積
が現れています。本問の場合、重心(円盤の中心)の移動距離は半径2の円周の長さに等しく 4π回転させる円盤の面積はπなので、4π×π= 4π 2となっているのです。