数学徒然草:Σ記号のこころ
Σ記号を苦手とする生徒さんが多いようですが:
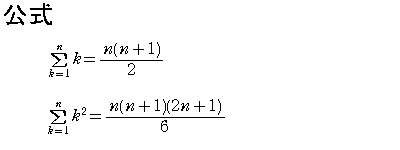
を機械的に覚えても柔軟性に欠け意味がありません。ここではΣ記号の定義自体を振り返ってみましょう。
そもそも:
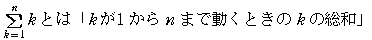
を意味します。具体的に書き下すと:

のようになります。同様に:

を意味します。具体的に書き下すと:
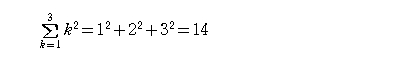
のようになります。
ここで計算結果にkが現れないことに注意して下さい。kは数を次々に代入するための箱の名前であって、何でもよい文字だったのです。ですから:

のように、k がl 、★、鬱 に替わっても式自体の意味は変わりません。(このような文字を内部変数といいます。定積分

の積分変数も内部変数ですね。) 以下、感覚的な例を挙げてみます:


Σ記号が4つもありますが、絡まった糸をほどくように、1つ1つ上記の原理に従って、書き下していきましょう。
(1) まず外側から、i の部分に 0 と 1 を入れて足せばよいのです。(それ以外の部分はそっくりそのままに。)

0-1=-1、1-1=0 です。
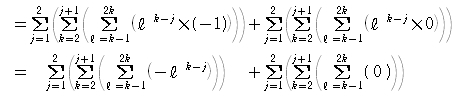
第2項は 0 を 足していくことになるので、結局、0 になります。

(2) 1つ目は解決しました。次にいきましょう。j の部分に 1 と 2を入れて足せばよいのです。(それ以外の部分はそっくりそのままに。)
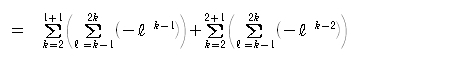
1+1=2、2+1=3 です。
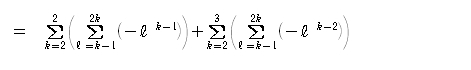
(3) 2つ目まで解決しました。次にいきましょう。第1項は、k の部分に 2 だけを、第2項は、k の部分に 2 と 3 を入れて足せばよいのです。(それ以外の部分はそっくりそのままに。)

2×2=4、2×2=4、2×3=6 です。

文字の1乗はそれ自身、0乗は数字の1になります。
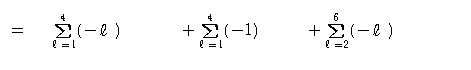
Σ記号の内部の定数倍は、Σ記号の外に出せます。
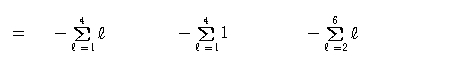
(4) 3つ目まで解決しました。だいぶすっきりしましたね。さて最後の詰めにいきましょう。第1項は、l の部分に 1 から 4 までを、第2項は、l の部分に 1 から 4 までを、(といっても入れるべきl がないので、1は1のまま)第3項は、l の部分に 2 から 6 までを入れて足せばよいのです。(それ以外の部分はそっくりそのままに。)
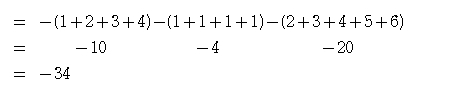
ということで、答えは -34 でした。如何でしたか? 一歩一歩着実に計算していけば、難なく計算できましたね。